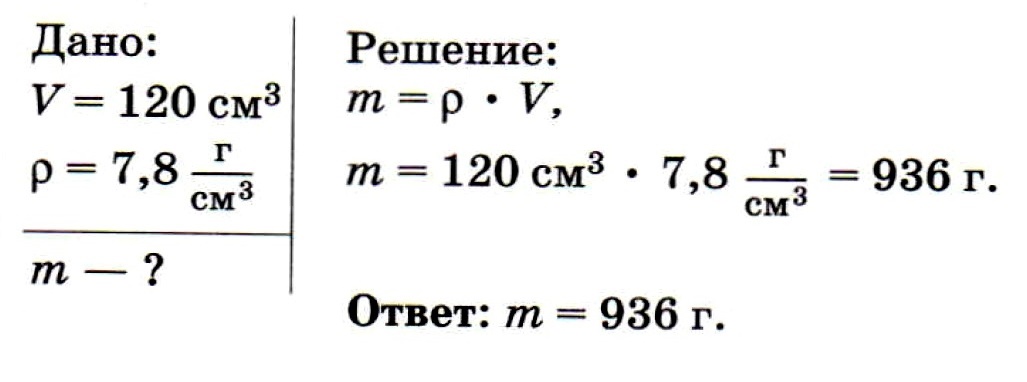Чему равен объем льда если его масса 2 кг

Льдина плавает в воде. Объём её надводной части равен 20 м 3 . Каков объём подводной части льдины? Плотность льда — 900 кг/м 3 , а плотность воды — 1000 кг/м 3 . Сделайте рисунок с указанием сил, действующих на льдину.

Льдина плавает в воде, следовательно, сила тяжести, действующая на неё, уравновешивается силой Архимеда:

Массу льдины можно найти как произведение плотности льда на объём льдины:

Сила Архимеда вычисляется как произведение плотности воды на объём подводной части льдины и на ускорение свободного падения:

Подставляя полученные выражения в первую формулу получаем:

Критерии оценивания выполнения задания

Баллы

I) Верно изображены силы (направление и масштаб), действующие на льдину.

II) Верно записаны: условие равновесия льдины; формула связи плотности, объёма и массы тела; формула силы Архимеда.

Источник

Чему равен объем льда если его масса 2 кг

Формулы, используемые в задачах по физике на плотность, массу и объем.

Название величины

Обозначение

Единицы измерения

Формула

Масса

m = p * V

Объем

V = m / p

Плотность

кг/м 3

p = m / V

Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

Физика 7 класс: все формулы и определения КРУПНО на трех страницах

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см 3 ?

Задача № 2. Определите объем кирпича, если его масса 5 кг?

Задача № 3. Определите массу стальной детали объёмом 120 см 3

Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м 3 ) меньше плотности стали (ρ₁ = 7800 кг/м 3 ). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

Задача № 5. Определите плотность мела, если масса его куска объемом 20 см 3 равна 48 г. Выразите эту плотность в кг/м 3 и в г/см 3 .

Ответ: Плотность мела 2,4 г/см 3 , или 2400 кг/м 3 .

Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м 2 ?

ОТВЕТ: 160 кг.

РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.

Вычисляем: m = 800 кг/м 3 • 0,04 м 2 • 5 м = 160 кг.

Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

РЕШЕНИЕ: Объем кубика V_K = а 3 = 216 см 3 . Объем стенок V_С можно вычислить, зная массу кубика m_К и плотность меди р: V_С = m_К / р = 91 см 3 . Следовательно, объем полости V_П = V_K — V_C = 125 см 3 . Поскольку 125 см 3 = (5 см) 3 , полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.

Задача № 9 (олимпиадный уровень). Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м 3

РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.

Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

Справочный материал для «Задачи на плотность, массу и объем«

Как, зная только массу, рассчитать плотность?

Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

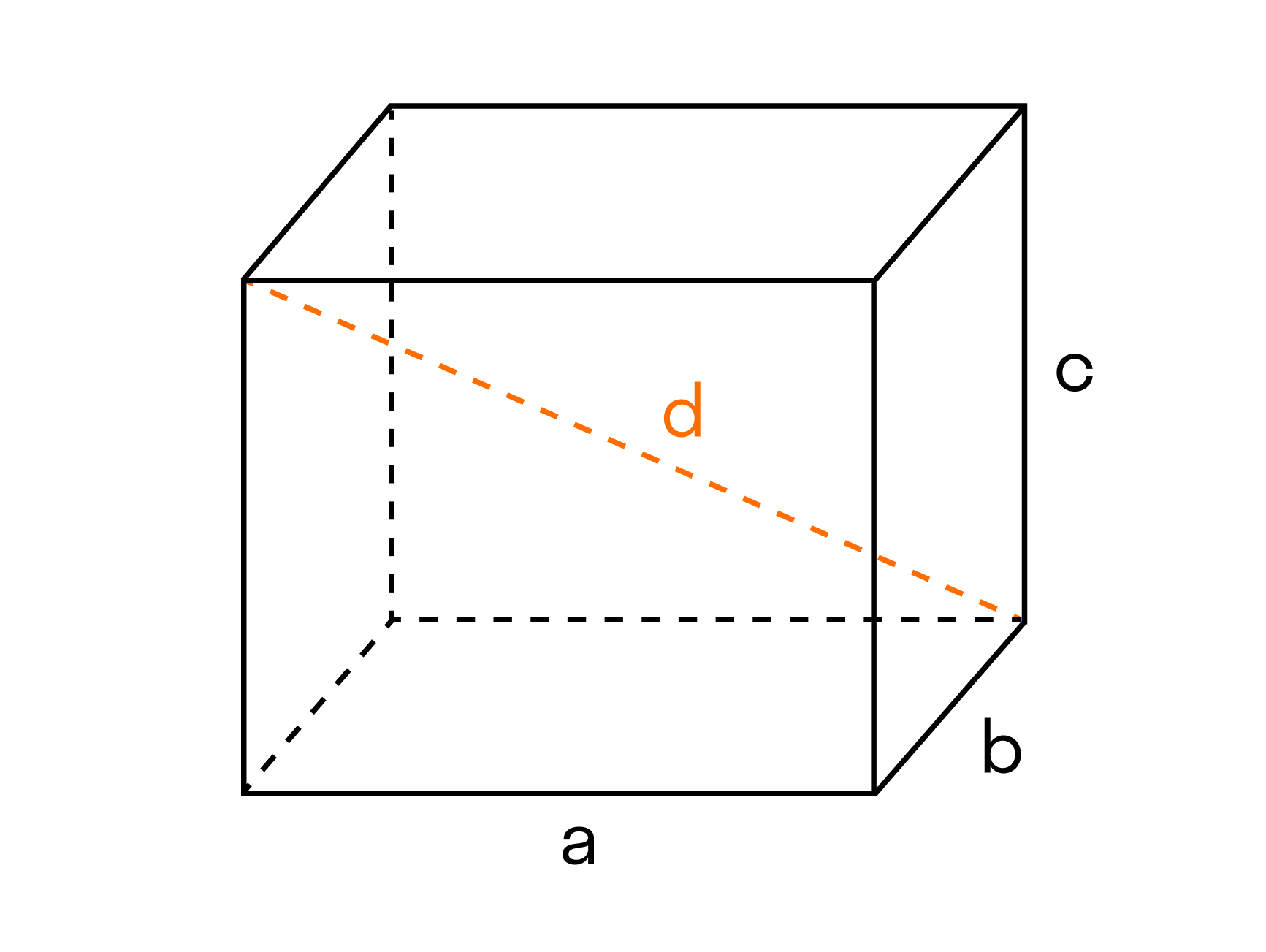
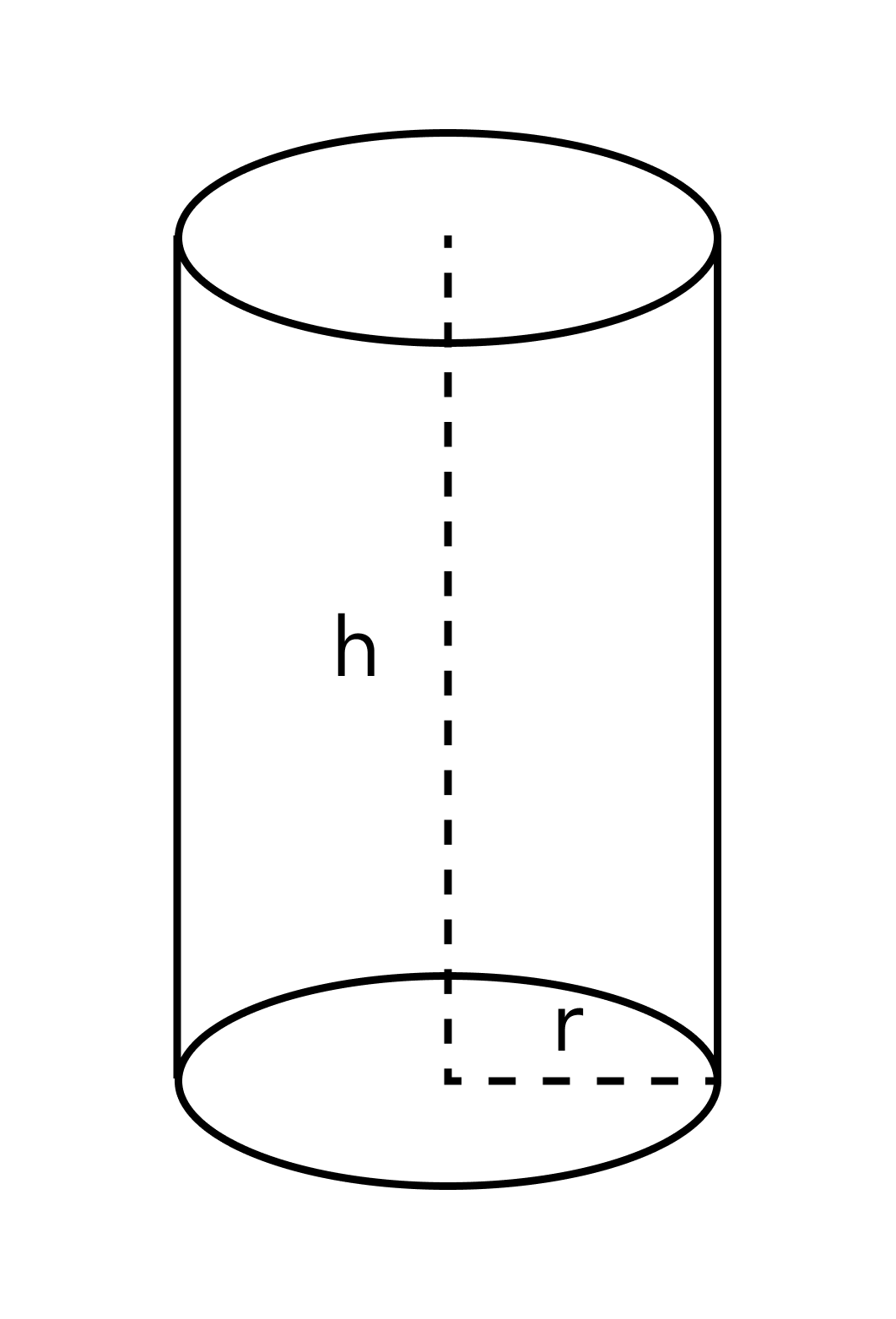
Конспект урока «Задачи на плотность, массу и объем с решением».

Источник

Плотность вещества

О чем эта статья:

Масса

Начнем с самого сложного — с массы. Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.

В Международном бюро мер и весов в Париже есть цилиндр массой один килограмм. Материал этого цилиндра — сплав иридия и платины. Его масса равна одному килограмму, и этот цилиндр — эталон для всего мира.

Высота этого цилиндра приблизительно равна 4 см, но чтобы его поднять, нужно приложить немалую силу. Необходимость эту силу прикладывать обуславливается инерцией тел и математически записывается через второй закон Ньютона.

Второй закон Ньютона

F = ma

a — ускорение [м/с2]

В этом законе массу можно считать неким коэффициентом, который связывает ускорение и силу. Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.

Закон Всемирного тяготения

F = GMm/R2

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

G = 6.67 × 10-11 м3 кг-1 с-2

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне🙃

Откуда берется масса

Физики убеждены, что у элементарных частиц должна быть масса. Доказано, что у электрона, например, масса есть. В противном случае они не могли бы образовать атомы и всю видимую материю.

Вселенная без массы представляла бы собой хаос из различных излучений, двигающихся со скоростью света. Не существовало бы ни галактик, ни звезд, ни планет. Здорово, что это не так, и у элементарных частиц есть масса. Только вот пока непонятно, откуда эта масса у них берется.

Мужчину на этой фотографии зовут Питер Хиггс. Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.

Бозон Хиггса невозможно представить. Это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.

Объем тела

Объем — это физическая величина, которая показывает, сколько пространства занимает тело. Это важный навык — уметь объемы соотносить. Например, чтобы посчитать, сколько пластиковых шариков помещается в гигантский бассейн.

Например, чтобы рассчитать объем прямоугольного параллелепипеда, нам нужно перемножить три его параметра.

Формула объема параллелепипеда

V = a*b*c

А для цилиндра будет справедлива такая формула:

Формула объема цилиндра

V = S*h

S — площадь основания [м^2]

Плотность вещества

Плотность — скалярная физическая величина. Определяется как отношение массы тела к занимаемому этим телом объёму.

Формула плотности вещества

р — плотность вещества [кг/м^3]

m — масса вещества [кг]

V — объем вещества [м^3]

Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.

Ниже представлены значения плотностей для разных веществ. В дальнейшем это поможет при решении задач.

Источник

Чему равен объем льда если его масса 2 кг

Железный шарик радиусом r = 1 см вморожен в ледяной шар радиусом R = 3 см. Их охладили до температуры t₁ = –20 °C и опустили в калориметр, в котором находится вода массой m = 270 г при температуре t₂ = +30 °C. Какая температура t установится в калориметре после достижения равновесного состояния? Потерями теплоты пренебречь. Плотность льда ρ_л = 900 кг/м 3 .

1. Во время теплообмена и установления теплового равновесия в калориметре тёплая вода будет охлаждаться, отдавая теплоту шару изо льда с вмороженным в него железным шариком. Часть этой теплоты пойдёт на нагревание шара до 0 °C, а оставшаяся — на плавление льда при 0 °C и возможное нагревание системы до некоторой положительной температуры, если теплоты охлаждения воды будет достаточно для этого.

2. Вначале найдём количество теплоты, которое может отдать тёплая вода при охлаждении до 0 °C:

(здесь — удельная теплоёмкость воды).

3. Затем найдём количество теплоты, необходимое для нагревания составного шара и плавления всего льда при 0 °C. Для этого вначале найдём массу железа и льда : (здесь — плотность железа); Далее имеем:

(здесь и — удельная теплоёмкость железа и льда, — удельная теплота плавления льда).

4. Таким образом, так что весь лёд при 0 °C не растает, и в равновесии установится температура t = 0 °C.

Критерии оценивания выполнения задания

Баллы

Приведено полное решение, включающее следующие элементы:

I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: уравнение теплового баланса, связь массы с плотностью и объемом, выражения для количества теплоты при нагревании и охлаждении тел, а также при плавлении тел);

II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов);

III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);

IV) представлен правильный ответ с указанием единиц измерения искомой величины

Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.

В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).

В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.

Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих случаев.

Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Источник

Читайте также: Куда уходят черви зимой