Чему равна удельная теплоемкость льда что это означает

Удельная теплоемкость вещества

О чем эта статья:

Нагревание и охлаждение

Эти два процесса знакомы каждому. Вот нам захотелось чайку, и мы ставим чайник, чтобы нагреть воду. Или ставим газировку в холодильник, чтобы охладить.

Логично предположить, что нагревание — это увеличение температуры, а охлаждение — ее уменьшение. Все, процесс понятен, едем дальше.

Но не тут-то было: температура меняется не «с потолка». Все завязано на таком понятии, как количество теплоты. При нагревании тело получает количество теплоты, а при нагревании — отдает.

• Количество теплоты — энергия, которую получает или теряет тело при теплопередаче.

В процессах нагревания и охлаждения формулы для количества теплоты выглядят так:

Нагревание

Охлаждение

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

В этих формулах фигурирует и изменение температуры, о котором мы сказали выше, и удельная теплоемкость, речь о которой пойдет дальше.

А вот теперь поговорим о видах теплопередачи.

Виды теплопередачи

• Теплопередача — это физический процесс передачи тепловой энергии от более нагретого тела к менее нагретому.

Здесь все совсем несложно, их всего три: теплопроводность, конвекция и излучение.

Теплопроводность

Тот вид теплопередачи, который можно охарактеризовать, как способность тел проводить энергию от более нагретого тела к менее нагретому.

Речь о том, чтобы передать тепло с помощью соприкосновения. Признавайтесь, грелись же когда-нибудь возле батареи. Если вы сидели к ней вплотную, то согрелись вы благодаря теплопроводности. Обниматься с котиком, у которого горячее пузо, тоже эффективно.

Порой мы немного перебарщиваем с возможностями этого эффекта, когда на пляже ложимся на горячий песок. Эффект есть, только не очень приятный. Ну а ледяная грелка на лбу дает обратный эффект — ваш лоб отдает тепло грелке.

Конвекция

Когда мы говорили о теплопроводности, мы приводили в пример батарею. Теплопроводность — это когда мы получаем тепло, прикоснувшись к батарее. Но все вещи в комнате к батарее не прикасаются, а комната греется. Здесь вступает конвекция.

Дело в том, что холодный воздух тяжелее горячего (холодный просто плотнее). Когда батарея нагревает некий объем воздуха, он тут же поднимается наверх, проходит вдоль потолка, успевает остыть и спуститься обратно вниз — к батарее, где снова нагревается. Таким образом, вся комната равномерно прогревается, потому что все более горячие потоки сменяют все менее холодные.

Излучение

Пляж мы уже упоминали, но речь шла только о горячем песочке. А вот тепло от солнышка — это излучение. В этом случае тепло передается через волны.

Обоими способами. То тепло, которое мы ощущаем непосредственно от камина (когда лицу горячо, если вы расположились слишком близко к камину) — это излучение. А вот прогревание комнаты в целом — это конвекция.

Удельная теплоемкость: понятие и формула для расчета

Формулы количества теплоты для нагревания и охлаждения мы уже разбирали, но давайте еще раз:

Нагревание

Охлаждение

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

В этих формулах фигурирует такая величина, как удельная теплоемкость. По сути своей — это способность материала получать или отдавать тепло.

С точки зрения математики удельная теплоемкость вещества — это количество теплоты, которое надо к нему подвести, чтобы изменить температуру 1 кг вещества на 1 градус Цельсия:

Удельная теплоемкость вещества

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

Также ее можно рассчитать через теплоемкость вещества:

Удельная теплоемкость вещества

c — удельная теплоемкость вещества [Дж/кг*˚C]

C — теплоемкость вещества [Дж/˚C]

Величины теплоемкость и удельная теплоемкость означают практически одно и то же. Отличие в том, что теплоемкость — это способность всего вещества к передаче тепла. То есть формулу количества теплоты для нагревания тела можно записать в таком виде:

Количество теплоты, необходимое для нагревания тела

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

Таблица удельных теплоемкостей

Удельная теплоемкость — табличная величина. Часто ее указывают в условии задачи, но при отсутствии в условии — можно и нужно воспользоваться таблицей. Ниже приведена таблица удельных теплоемкостей для некоторых (многих) веществ.

Источник

Удельная теплоёмкость

Уде́льная теплоёмкость — физическая величина, численно равная количеству теплоты, которое необходимо передать телу массой 1 кг для того, чтобы его температура изменилась на 1 Кельвин. Удельная теплоемкость обозначается буквой c и измеряется в Дж/кг*Кельвин.

Единицей СИ для удельной теплоёмкости является джоуль на килограмм-кельвин. Следовательно, удельную теплоёмкость можно рассматривать как теплоёмкость единицы массы вещества. На значение удельной теплоёмкости влияет температура вещества. К примеру, измерение удельной теплоёмкости воды даст разные результаты при 20 °C и 60 °C.

Формула расчёта удельной теплоёмкости: , где — удельная теплоёмкость, — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении), — масса нагреваемого (охлаждающегося) вещества, — разность конечной и начальной температур вещества.

Источник

Удельная теплоемкость

Содержание

Вам уже известно, что количество теплоты зависит от массы вещества, разности температур и рода вещества. Количество теплоты ($Q$) в СИ измеряется в джоулях ($Дж$).

Возьмем два тела одинаковой массы и температуры, но из разных веществ. Логично, что для их нагрева на $1 \degree C$ потребуется разное количество теплоты. В этом случае у нас разный род веществ, из которых состоят тела. Здесь мы вводим новое понятие – удельная теплоемкость вещества.

В данном уроке мы рассмотрим это новое для нас определение, узнаем его физическое значение, познакомимся с удельной теплоемкостью различных веществ.

Удельная теплоемкость вещества

Удельная теплоемкость вещества – это физическая величина, численно равная количеству теплоты, которое необходимо передать телу массой $1 \space кг$ для того, чтобы его температура изменилась на $1 \degree C$

Рассмотрим на примерах, как удельная теплоемкость характеризует вещество.

Возьмем $1 \space кг$ воды и нагреем его на $1 \degree C$ (рисунок 1).

Для этого нам понадобится $4200 \space Дж$. Именно это количество теплоты и будет определять удельную теплоемкость воды.

А теперь нагреем на $1 \degree C$ кусок свинца массой $1 \space кг$ (рисунок 2).

В этот раз нам потребуется затратить $140 \space Дж$. Это значение ожидаемо отличается от количества теплоты, затраченное на нагревание воды. Тем не менее, это количество теплоты так же будет характеризовать удельную теплоемкость свинца.

Единица измерения удельной теплоемкости

Удельная теплоемкость обозначается буквой $c$.

Измеряется удельная теплоемкость вещества в $\frac<Дж><кг \cdot \degree C>$.

Рассмотрим эту единицу измерения на примере графита. Его удельная теплоемкость равна $750 \frac<Дж><кг \cdot \degree C>$. Что это означает?

Из этого значения мы можем сказать, что:

1. Для нагревания куска графита массой $1 \space кг$ на $1 \degree C$ нам необходимо затратить количество теплоты, равное $750 \space Дж$
2. При охлаждении куска графиты массой $1 \space кг$ на $1 \degree C$ будет выделяться количество теплоты, равное $750 \space Дж$
3. При изменении температуры куска графита массой $1 \space кг$ на $1 \degree C$ он будет или поглощать, или выделять количество теплоты, равное $750 \space Дж$

Табличные значения удельной теплоемкости

Существуют уже известные значения удельной теплоемкости различных веществ. Они представлены таблице 1.

Вещество	$c, \frac<Дж><кг \cdot \degree C>$	Вещество	$c, \frac<Дж><кг \cdot \degree C>$
Золото	130	Песок	820
Ртуть	140	Стекло	840
Свинец	140	Кирпич	880
Олово	230	Алюминий	920
Серебро	250	Масло подсолнечное	1700
Медь	400	Лед	2100
Цинк	400	Керосин	2100
Латунь	400	Эфир	2350
Железо	460	Дерево (дуб)	2400
Сталь	500	Спирт	2500
Чугун	540	Вода	4200
Графит	750	Гелий	5200

Таблица 1. Удельные теплоемкости некоторых веществ.

Вода имеет почти самую большую теплоемкость в таблице – $4200 \frac<Дж><кг \cdot \degree C>$. Это означает, что вода, находящаяся в морях и океанах, поглощает большое количество теплоты, нагреваясь летом. Зимой воды начинает остывать и отдавать большое количество теплоты. Поэтому, в местностях, которые расположены в непосредственной близости от воды, летом не бывает очень жарко, а зимой не бывает очень холодно. По этой же причине воду широко используют в технике (например, охлаждение деталей во время их обработки) и быту (отопительный системы помещений).

Песок имеет небольшую теплоемкость – $820 \frac<Дж><кг \cdot \degree C>$. Он быстро нагревается и быстро остывает. Поэтому в пустыне днем очень жарко, а ночью температура может опуститься почти ниже $0 \degree C$.

Удельная теплоемкость и агрегатные состояния вещества

Давайте взглянем в таблицу 1 и сравним значения удельной теплоемкости льда и воды.

Удельная теплоемкость льда – $ 2100 \frac<Дж><кг \cdot \degree C>$, а воды – $4200 \frac<Дж><кг \cdot \degree C>$. Но мы знаем, что одно и то же вещество в разных агрегатных состояниях.

Удельная теплоемкость вещества, находящегося в различных агрегатных состояниях, различна.

Например, при $-120 \degree C$ ртуть будет находиться в твердом состоянии. Ее удельная теплоемкость будет равна $129 \frac<Дж><кг \cdot \degree C>$. В жидком же состоянии удельная теплоемкость ртути равна $138 \frac<Дж><кг \cdot \degree C>$.

Источник

Плотность льда и снега, теплопроводность, теплоемкость льда

Плотность, теплопроводность и теплоемкость льда в зависимости от температуры

В таблице приведены значения плотности, теплопроводности, удельной теплоемкости льда в зависимости от температуры в интервале от 0 до -100°С.

По данным таблицы видно, что с понижением температуры удельная теплоемкость льда уменьшается, а теплопроводность и плотность льда, напротив, растут. Например, при температуре 0°С плотность льда имеет значение 916,2 кг/м 3 , а при температуре минус 100°С его плотность становится равной 925,7 кг/м 3 .

Значение удельной теплоемкости льда при 0°С составляет 2050 Дж/(кг·град). При снижении температуры льда с -5 до -100°С его удельная теплоемкость снижается в 1,45 раза. Теплоемкость льда в два раза меньше значения этой величины у воды.

Теплопроводность льда при понижении его температуры с 0 до минус 100°С увеличивается с 2,22 до 3,48 Вт/(м·град). Лед более теплопроводен, чем вода — он может проводить в 4 раза больше тепла при одинаковых граничных условиях.

Следует отметить, что плотность льда меньше плотности воды, однако с понижением температуры плотность льда растет и при приближении к абсолютному нулю температуры плотность льда становится близка к величине плотности воды.

Таблица плотности, теплопроводности и теплоемкости льда

Температура, °С	Плотность, кг/м 3	Теплопроводность, Вт/(м·град)	Теплоемкость, Дж/(кг·град)
0.01 (Вода)	999,8	0,56	4212
0	916,2	2,22	2050
-5	917,5	2,25	2027
-10	918,9	2,30	2000
-15	919,4	2,34	1972
-20	919,4	2,39	1943
-25	919,6	2,45	1913
-30	920,0	2,50	1882
-35	920,4	2,57	1851
-40	920,8	2,63	1818
-50	921,6	2,76	1751
-60	922,4	2,90	1681
-70	923,3	3,05	1609
-80	924,1	3,19	1536
-90	924,9	3,34	1463
-100	925,7	3,48	1389

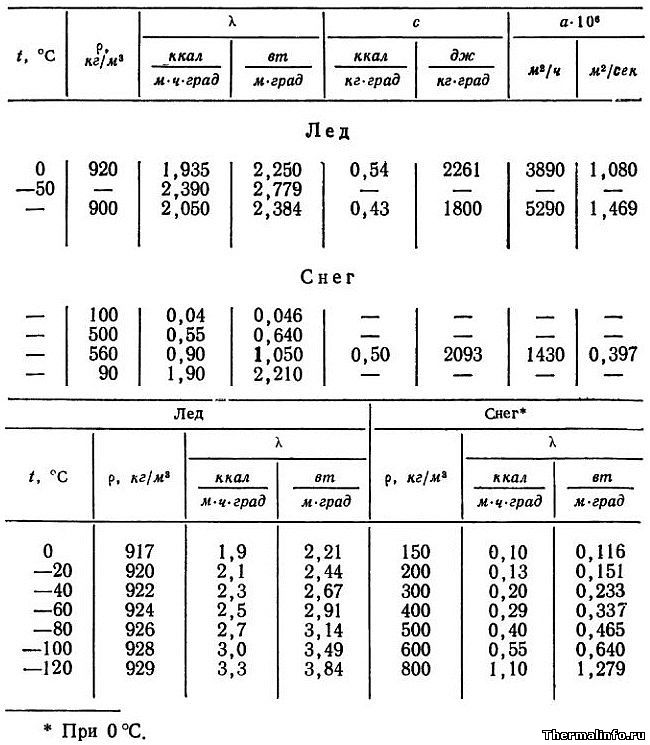
Теплофизические свойства льда и снега

В таблице представлены следующие свойства льда и снега:

• плотность льда, кг/м 3 ;
• теплопроводность льда и снега, ккал/(м·час·град) и Вт/(м·град);
• удельная массовая теплоемкость льда, ккал/(кг·град) и Дж/кг·град);
• коэффициент температуропроводности, м 2 /час и м 2 /сек.

Свойства льда и снега представлены в зависимости от температуры в интервале: для льда от 0 до -120°С; для снега от 0 до -50°С в зависимости от уплотненности (плотности). Температуропроводность льда и снега в таблице приведена с множителем 10 6 . Например, температуропроводность льда при температуре 0°С равна 1,08·10 -6 м 2 /с.

Давление насыщенного пара льда

В таблице приведены значения давления насыщенного пара льда при сублимации (переход льда в пар, миную жидкую фазу) в зависимости от температуры в интервале от 0,01 до -80°С. Из таблицы видно, что с понижением температуры льда давление его насыщенного пара снижается.

Источник