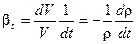Коэффициент объемного расширения льда

Содержание

Физико-механические и теплофизические свойства льда и шуги
Физико-механические и теплофизические свойства льда и шуги
Расширение воды при замерзании

Физико-механические и теплофизические свойства льда и шуги

Плотность льда, образовавшегося при кристаллизации пресной воды при 0°С и нормальном давлении, составляет в среднем 917 кг/м 3 . Следовательно, плотность пресноводного льда меньше плотности воды. Плотность льда зависит от его структуры, температуры и в большей степени от его пористости (во льду рек и водоемов почти всегда наблюдаются пузырьки воздуха).

С понижением температуры плотность льда увеличивается, а объем уменьшается. В зависимости от температуры плотность и удельный объем льда можно рассчитать по формулам Вейнберга:

ρ = 917 (1 — 0,000158t)(1 — n); (2.33)

где п — пористость льда.

Из (2.33) следует, что, зная плотность льда (r_л,_n₌₀.=917кг/м 3 ), можно определить его пористость

Плотность льда, образовавшегося в результате замерзания соленой воды(морской или озерной), зависит не только от его температуры и количества воздушных пузырьков в нем, но еще и от содержания солей в прослойках между кристаллами льда и от количества в этих прослойках рассола. И то и другое зависит от быстроты замерзания и от возраста льда. Старый морской лед имеет иное распределение солености по глубине, чем молодой. В морском льду рассол стекает вниз по неизбежным во льду трещинам, вследствие чего соленость его непрерывно изменяется во времени. Соленость льда всегда меньше солености воды, из которой он образовался.

Плотность морского льда увеличивается по мере увеличения солености воды и уменьшается с увеличением содержания воздушных пузырьков.

Расширение (сжатие) характеризуется коэффициентом объемного расширения, который равен отношению относительного изменения объема вещества V к изменению температуры t и определяется по формуле

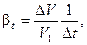
Коэффициент объемного расширения (сжатия) льда β_t можно принять с достаточно высокой точностью постоянным и равным

0,158·10 -3 °С -1 . Коэффициент линейного расширения (сжатия) соответственно равен a_t = β_t/3 = 0,053·10 -3 °С -1 .

Лед течет при напряжениях в ледяном покрове P > 5·10 4 Па. Характеристикой его текучести является коэффициент вязкости μ. Этот коэффициент определяется в зависимости от температуры льда по формулам:

при t ≥ -20°С

μ = (11,6 – 0,978t +0,293t 2 ) 10 11 , (2.35)

при t 11 , (2.36)

где t — средняя температура слоя льда.

ДЛЯ ВОДЫ при t = 0 0 μ = 1,793·10 3 Па·с

Коэффициент μ также сильно зависит от структуры льда, характера нагрузки и продолжительности ее приложения.

Плавление льда при постоянном внешнем давлении протекает при определенной температуре, называемой температурой плавления — t_пл.

Температура плавления льда определяется давлением, при котором он находится; она понижается с повышением давления (рис. 2.2). Зависимость ее от давления описывается уравнением Клапейрона—Клаузиуса, а также может быть представлена следующей формулой:

(2.37)

При давлении до 10 7 Па эту зависимость можно заменить линейной:

Рис. 2.2. Ход температуры во льду во времени при подводе к нему теплоты [8]

1 — 2 — нагревание льда; 2 — 3 — плавление льда: 3 — 4— нагревание воды; t_пл —температура плавления льда.

Плавление льда при атмосферном давлении происходит при температуре 0,01°С (в практических расчетах принимают 0°С).Количество теплоты, которое необходимо сообщить 1 кг льда, находящемуся при температуре плавления, для превращения его в воду, называют удельной теплотой плавления L_пл. Удельная теплота плавления пресноводного льда при нормальных условиях равна удельной теплоте кристаллизации воды 33,3·10 4 Дж/кг (п. 2.1).

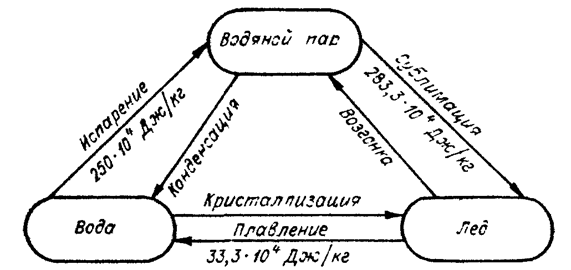
Удельная теплота сублимации (возгонки) льда (рис. 2.3) равна сумме удельной теплоты плавления льда и удельной теплоты испарения воды; при 0°С она равна

L_воз = 33,3·10 4 + 250·10 4 = 283,3·10 4 Дж/кг.

Коэффициент теплопроводности льда λ принимают в среднем равным 2,24Вт/(м·°С). С повышением температуры λуменьшается незначительно и линейно.

Удельную теплоемкость льда вычисляют по формуле Б. П. Вейнберга:

c = 2,12 (1 + 0,0037t). (2.39)

При t=0°С теплоемкость льда c = 2,12 кДж/(кг·°С).

Рис. 2.3. Схема изменения агрегатного состояния воды [8]

Таблица 2.4

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)

Источник

Физико-механические и теплофизические свойства льда и шуги

Плотность льда, образовавшегося при кристаллизации пресной воды при 0°С и нормальном давлении, составляет в среднем 917 кг/м 3 . Следовательно, плотность пресноводного льда меньше плотности воды. Плотность льда зависит от его структуры, температуры и в большей степени от его пористости (во льду рек и водоемов почти всегда наблюдаются пузырьки воздуха).

С понижением температуры плотность льда увеличивается, а объем уменьшается. В зависимости от температуры плотность и удельный объем льда можно рассчитать по формулам Вейнберга:

ρ = 917 (1 — 0,000158t)(1 — n); (2.33)

где п — пористость льда.

Из (2.33) следует, что, зная плотность льда (r_л,_n₌₀.=917кг/м 3 ), можно определить его пористость

Плотность льда, образовавшегося в результате замерзания соленой воды (морской или озерной), зависит не только от его температуры и количества воздушных пузырьков в нем, но еще и от содержания солей в прослойках между кристаллами льда и от количества в этих прослойках рассола. И то и другое зависит от быстроты замерзания и от возраста льда. Старый морской лед имеет иное распределение солености по глубине, чем молодой. В морском льду рассол стекает вниз по неизбежным во льду трещинам, вследствие чего соленость его непрерывно изменяется во времени. Соленость льда всегда меньше солености воды, из которой он образовался.

Изменение плотности льда при изменении давления характеризуется коэффициентом сжимаемости β. Например, при изменении давления в интервале (1 . 5) · 10 7 Па при t = — 7°С β = 1,2·10 -10 1/Па.

Коэффициент объемного расширения (сжатия) льда β_t можно принять с достаточно высокой точностью постоянным и равным 0,158·10 -3 °С -1 . Коэффициент линейного расширения (сжатия) соответственно равен a_t = β_t/3 = 0,053·10 -3 °С -1 .

Лед течет при напряжениях в ледяном покрове P > 5·10 4 Па. Характеристикой его текучести является коэффициент вязкости μ. Этот коэффициент определяется в зависимости от температуры льда по формулам:

μ = (11,6 – 0,978t +0,293t 2 ) 10 11 , (2.35)

где t — средняя температура слоя льда.

Коэффициент μ также сильно зависит от структуры льда, характера нагрузки и продолжительности ее приложения.

Температура плавления льда определяется давлением, при котором он находится; она понижается с повышением давления (рис. 2.2). Зависимость ее от давления описывается уравнением Клапейрона—Клаузиуса, а также может быть представлена следующей формулой:

(2.37)

При давлении до 10 7 Па эту зависимость можно заменить линейной:

Рис. 2.2. Ход температуры во льду во времени при подводе к нему теплоты [8]

1 — 2 — нагревание льда; 2 — 3 — плавление льда: 3 — 4— нагревание воды; t_пл —температура плавления льда.

Плавление льда при атмосферном давлении происходит при температуре 0,01°С (в практических расчетах принимают 0°С). Количество теплоты, которое необходимо сообщить 1 кг льда, находящемуся при температуре плавления, для превращения его в воду, называют удельной теплотой плавления L_пл. Удельная теплота плавления пресноводного льда при нормальных условиях равна удельной теплоте кристаллизации воды 33,3·10 4 Дж/кг (п. 2.1).

Удельная теплота сублимации (возгонки) льда (рис. 2.3) равна сумме удельной теплоты плавления льда и удельной теплоты испарения воды; при 0°С она равна L_воз = 33,3·10 4 + 250·10 4 = 283,3·10 4 Дж/кг.

Коэффициент теплопроводности льда λ принимают в среднем равным 2,24Вт/(м·°С). С повышением температуры λ уменьшается незначительно и линейно.

Удельную теплоемкость льда вычисляют по формуле Б. П. Вейнберга:

Учитывая, что при t=0°С плотность льда ρ = 917 кг/м 3 , а удельная теплоемкость его c = 2,12 кДж/(кг·°С), получаем коэффициент температуропроводности льда при нормальных условиях a = λ/(cρ)=2,24/(2,12·917) = 4,1·10 -3 м 2 /ч.

Рис. 2.3. Схема изменения агрегатного состояния воды [8]

С понижением температуры коэффициент a существенно повышается, так как при этом не только увеличивается λ, но и уменьшается c:

a = 4,1(1 – 0,0063t) 10 -3 . (2.40)

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Расширение воды при замерзании

Наступает зима, а вместе с ней традиционно приходят аварии на водоопроводах. В сильные морозы основная причина таких аварий – замерзание текущей воды. При этом, как известно, происходит ее расширение, так что образующийся лед легко разрывает трубы (для справки: плотность льда – 917 кг/м 3 , плотность воды – 1000 кг/м 3 , то есть объем увеличивается в 1.1 раза, что довольно существенно). Аналогичное явление происходит, если на зиму оставить воду в емкостях с водой (например, на даче).

Для изучения данного явления в домашних условиях используем обычную консервную банку. В данной банке изначально было концентрированное молоко, которое было вылито через два аккуратно пробитых отверстия. Затем в банку заливается вода – так, чтобы внутри не осталось воздуха. Проще всего это сделать, погрузив ее в кастрюлю с водой. Когда из банки перестанет выходить воздух, она будет полностью заполнена водой.

После этого аккуратно запаиваем отверстия и помещаем нашу банку в морозильную камеру (зимой можно на улицу). Если подождать день-два, то станет хорошо заметно, как расширившаяся вода (лед) выдавила нижнюю крышку банки.

В качестве домашнего задания предлагаю следующие вопросы:

1. Почему замерзающая вода выдавливается именно нижнюю крышку, и практически не влияет на верхнюю? (хорошо видно на видео)

2. Что произойдет с банкой, если сейчас растопить лед, и снова заморозить? Если повторить такую процедуру несколько раз?

0lympian 16 ноября 2010, 12:41

Как запаять ПОЛНУЮ банку с водой? О_о

Ничего не получится – это уже опыт по теплопроводности и теплоемкости

0lympian

16 ноября 2010, 12:47

> 1. Почему замерзающая вода выдавливается именно нижнюю крышку, и практически не влияет на верхнюю?

Подозреваю, что в результате того, что лед легче незамерзшей воды, первые кристаллы льда всплывают, комбинируясь друг с другом и в верхней части замерзание происходит быстрее.

Стоит отметить, что с другой стороны, есть конвекция, которая будет действовать ровно наоборот, поднимая более теплую воду наверх, и препятствуя там ледообразованию. Однако мне кажется, что при медленном равномерном промерзании этот эффект нивелируется.

Ну а далее уже готовый лед, сформировавшийся в верхней части еще до сильного расширения, в некоторой степени «держит форму», не позволяя сильно деформироваться крышке.

0lympian

16 ноября 2010, 12:49

> 2. Что произойдет с банкой, если сейчас растопить лед, и снова заморозить?

Очевидно, что объем воды вернется к первоначальному. Однако за счет чего – тут есть предположение, что вдавится не донышко (оно сильно сводообразное стало), а боковая стенка банки.

Ну а при последующих циклах, пожалуй, баночка помнется еще сильнее, пока не порвется

Administrator

16 ноября 2010, 19:07

Как запаять ПОЛНУЮ банку с водой?

Согласен. Идеальное запаивание тут не получается. Так, наляпывание припоя сверху, лишь бы вода не вытекала. Кстати, в месте пайки действительно образуется водяной пар при нагреве паяльником.

Если бы баночка была абсолютно герметична – тогда да, вдавилась бы боковая стенка. А так все равно воздух проникает. Поэтому после разморозки получается, что сверху появляется воздух, во время заморозки дно выдавливается еще сильнее, и так далее, пока совсем его не вырвет.

P. S. Сегодня разморозил банку, и поставил на второе замораживание. Посмотрим, что из этого получится.

владимир

16 ноября 2010, 20:32

1. пробовал запаять не выходит! смог только заварить полуавтоматом (электро–сваркой) заморозил, разморозил дно не втянулось подумал из–за воздуха, взял другую банку впаял пипку от камеры проверил воздухом на 2 атм утечек нет залил воды воздуха нет! заморозил разморозил бока почти не втянулись проверил через час появилось избыточное давление и мне кажется что при заморозке и разморозке воды выделяется растворенный в ней воздух потому и бока не втягиваются
2, вода кристаллизуется сверху (река зимой, бочка с водой) лед легче воды, думаю, что и холодно–проводность.

Administrator

17 ноября 2010, 14:53

Владимир, вы серьезно подошли к эксперименту. Не написали самое главное – какие банки брали, и что произошло с ними при заморозке воды.

владимир

17 ноября 2010, 21:27

банка такая же как и ваша из–под молока произошло все анологично как у вас после разморозки слегка спало напряжение размораживал при комнатной температуре мне кажется стоит учитывать температуру воды в моем случае это 7 градусов, а комнатная 25 градусов тоже наверное влияет. сейчас проверяю что будет если банки положить набок швом к верху и швом к низу!

Administrator

18 ноября 2010, 06:21

сейчас проверяю что будет если банки положить набок швом к верху и швом к низу!

Интересно! Дайте ссылки на фотографии результатов, если будет возможность.

Евгений

12 января 2011, 18:01

> 1. Почему замерзающая вода выдавливается именно нижнюю крышку, и практически не влияет на верхнюю?
Пологаю что процесс заморозки, учитывая то что банка находилась в пластиковой таре, протикал не ровномерно. Первым стала замерзать верхняя часть банки потому как она была ближе к холоду нижняя же часть нахоидась там где между стенками пластика и ж. банки находился воздух чуть теплее чем с верху. Далее обледенение внутр верхней части банки придовало ей дополнительную прочность но превращаясь в лед вода расширялась и давила на жидкость в нижней части ж. банки.

гражданина

13 июля 2011, 20:46

> 1. Почему замерзающая вода выдавливается именно нижнюю крышку, и практически не влияет на верхнюю?

1. лед образуется сверху. это обусловлено тем, что остывающая (а не замерзающая вода как пишет автор) поднимается к верху за счёт того что при остывании (от 4 градусов до 0) плотность уменьшается.
2. остывающая (а не замерзающая вода как пишет автор) за счет увеличения обьема давит уже не на крышку а на ледяную «шайбу» которая распределяет усилие по всей площади крышки равномерно. наиболее «слабая» часть крышки (от центра) подвергается такому же давлению что и наиболее «сильные» части (возле боковых стенок). вследствие этого усилие создаваемое остывающей водой гаситься «сильной» частью крышки. в нижней же части льда нет, вода давит на «сильные» части, они не прогибаются, общее давление переходит на «слабые» части, не поглощаясь «сильными» (потому что усилие через воду передается во всех направлениях). както вот так.

Wulkan

24 августа 2011, 08:24

Запаивание банки это все ерунда, на даче стояла бочка с водой без крышки, и к весне у нее выдавило днище. скорее всего промерзание идет сверху вниз и внизу создается избыточное давление. лед примерзший к стенкам не дает расширения вверх

Andrey

23 октября 2011, 04:17

Тов. Ученые! А может кто подскажет какое давление оказывает замерзающая вода и образовавшийся лед на стенки сосуда?

Scolar

4 ноября 2011, 12:27

Спасибо, интересный эксперимент! Особенно интересно, что именно нижняя крышка выдавилась. Интересно, это зависит от того, стоит ли банка на ней в морозильнике, или подвешена, к примеру, на пластиковых элементах? Существует также такой фактор, как плавление воды при повышении давления (зависит также от температуры), из–за чего коньки скользят по льду и т. д.

Kalstrams

1 мая 2012, 20:53

Не мудрите. Продавило низ, потому что гравитация работает и на эту банку + то, что с низу самая большая плотность воды при замерзании, по-этому не верху банально не было столько же массы для расширения, сколько ее было снизу.

Давление вычислит можно по p1/p2 = ((n вода)/(n лед))*T1/T2

Выдавится всегда нижняя крышка, разве что банка будет замерзать в условии постоянного вращения. Или в условии отсутствия воздействия гравитации.

Что-бы получить температуру льда для уравнения выше, мерим температуру банки, Q1=Q2, Q1=c*m*dT (банка)
Q2=c2*m2*dT2 + dL*m + c3*m2*dT3
вода охлаждается + вода кристаллизуется + лед охлаждается
dT3 = (c*m*dT-c2*m2*dT2-dL*m)/(c3*m2)

Это будет изменение температуры льда.
Подставите его в T=0+273-dT3 — будет температура Т2.
Температура T1 — воды — термометром когда вода войдет в термодинамическое равновесие с банкой.

p2 — давление льда, p1=pa+((m*9.8)/S(дна))

Вроде бы и все.
Получите p2, который будет равен величине давления, необходимого что-бы выдавить вашу банку на сколько-то.

В упрощенной форме эта задача выглядит так, и результат не абсолютно точен. Для точности тут надо было-бы проинтегрировать, да думаю это перебор.

Источник