исследовательская работа «по чему скользят сани и почему»
исследовательская работа, представленная на конкурсе младших школьников «Я- исследователь» , секция «физика-техника», вторая возрастная группа.
Скачать:
| Вложение | Размер |
|---|---|
| творческая работа | 54.5 КБ |
Предварительный просмотр:
Здравствуйте, меня зовут Даша, я учусь во 2-ом классе Хирпосинской основной общеобразовательной школы.
Однажды летом моя маленькая сестрёнка увидела в кладовке убранные на лето сани и стала интересоваться . Она задала несколько интересных вопросов.
Вопрос первый : что такое сани, когда они появились?
Вопрос второй: А почему сани скользят?
С этим вопросом я обратилась к маме, когда мы возвращались с санной прогулки домой. Мне стало очень интересно, что же позволяет саням скользить так легко. Оказывается, когда мы сидим на санках, мы опираемся на маленькую площадь, давим своим весом на небольшую площадь, а при движении полозья трутся о снег. При быстром движении под большим давлением снег под полозьями нагревается и начинает таять. Таким образом, между полозьями санок и слоем снега появляется тонкий слой воды. Вода позволяет скользить металлическим полозьям по снегу легко, потому что служит смазкой для полозьев и уменьшает трение. Следовательно, можно сделать вывод: скользкость саней зависит от температуры снега и скорости перемещения саней.
Зимой, когда катаемся, часто наблюдаем, как санки, скатившись с горы, через некоторое время останавливаются. Мальчик, разбежавшись, скользит на коньках по льду, но, как бы ни был гладок лёд, мальчик все-таки останавливается. Мы знаем, что причиной любого изменения скорости является сила. Значит, в рассмотренных примерах на каждое движущееся тело действовала сила. Сила, возникающая при движении одного тела по поверхности другого, называется слой трения. Поверхности тел имеют неровности, бугорки, царапины. Когда одно тело скользит по поверхности другого, эти неровности зацепляются друг за друга. Создается некоторая сила, задерживающая движение. Эту силу в физике называют трением скольжения. Вот такое трение и возникает при движении саней и лыж по снегу. Силу трения можно измерить. У меня появляется следующий вопрос.
Итак, вопрос третий: где легче скользить?
Чтобы определить силу трения скольжения мы провели некоторую работу с помощью динамометра. Динамометр-это специальный прибор для измерения силы. Для эксперимента мы взяли деревянные и железные сани и попытались прокатиться на них по снегу, льду, по земле и по асфальту. С помощью динамометра мы измерили силу трения скольжения саней по названным поверхностям, затем определили коэффициент трения. ( см. приложение). В результате получилось, что самый маленький показатель при скольжении стальных саней по снегу и льду. Значит, легче скользить на железных санях по снегу или по льду. Самый высокий коэффициент получается при скольжении деревянных саней по земле. Вот почему, оказывается, не принято пользоваться санями летом. В результате опыта мы смогли определить, что сила трения скольжения зависит от рода трущихся поверхностей, от шероховатости поверхностей, чем больше шероховатость, тем больше сила трения скольжения,и нам летом приходится тратить много сил, чтобы сдвинуть санки с места .
В результате проделанной работы я узнала следующее:
Сани появились во втором тысячелетии до нашей эры у народов Севера. С момента появления их устройство практически не изменилось.
Сани скользят, благодаря силе трения скольжения, при которой выделяется тепло. Скользкость саней зависит от температуры снега под полозьями и от скорости перемещения саней. Силу можно измерить с помощью специального прибора-динамометра.
Сила трения скольжения зависит и от рода, и от шероховатости трущихся поверхностей. Чем больше шероховатость, тем больше сила трения скольжения.
Все-таки, санями легче пользоваться зимой, чем летом.
- Громов С.В., Родина Н.А. Физика 7 класс-М.: Просвещение, 2000г.
- Кикоин И. К., Кикоин А. К. Физика 9 класс-М.: Просвещение,1990г.
- Ожегов С. И., Шведова Н.Ю. Толковый словарь русского языка-М.: ООО « А ТЕМП», 2010.
Источник
Коэффициент трения скольжения саней по снегу
Школьник скатывается на санках со склона оврага. Сначала он едет по шероховатому снегу, а потом въезжает на очень гладкий обледеневший участок склона. Угол наклона склона оврага к горизонту всюду одинаков. Как при этом изменяются следующие физические величины: модуль действующей на санки силы трения, модуль ускорения санок, модуль работы силы тяжести при перемещении санок вдоль склона на 1 метр?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ |

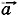 = m
= m 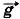 + N +
+ N + 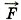 тp +
тp + 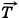 . (1)
. (1)  при этом
при этом 


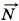 и сила трения
и сила трения 












