Стоящий льду человек ловит мяч

Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит

Условие задачи:

Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит горизонтально со скоростью 20 м/с. На какое расстояние откатился человек с мячом, если коэффициент трения равен 0,05?

Задача №2.10.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

\(M=60\) кг, \(m=0,5\) кг, \(\upsilon_0=20\) м/с, \(\mu=0,05\), \(S-?\)

Решение задачи:

На систему “человек – мяч” до удара и сразу после него не действуют горизонтальные силы, поэтому система замкнута вдоль оси \(x\). Это дает нам право воспользоваться законом сохранения импульса (в проекции на ось \(x\)):

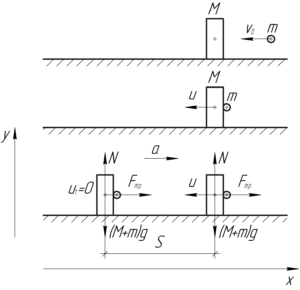
Выразим скорость человека с мячом сразу после удара \(u\):

Далее человек с мячом в руках начнёт равнозамедленное движение, поскольку на него будет действовать сила трения скольжения. Так как вдоль оси \(y\) человек не движется, то запишем первый закон Ньютона в проекции на эту ось:

Силу трения скольжения определяют по такой формуле:

Учитывая (2), имеем:

Применим второй закон Ньютона уже в проекции на ось \(x\):

Приравняем правые части (3) и (4) и выразим ускорение \(a\):

\[\left( \right)a = \mu \left( \right)g\]

В конце концов человек прекратит своё скольжение, пройдя перед этим расстояние \(S\). В кинематики доказывается, что справедливо следующее:

Подставим в последнюю формулу полученные ранее выражения (1) и (5), тогда решим задачу в общем виде:

Посчитаем численный ответ:

Ответ: 27 мм.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

А как решается задача если нужно найти массу мяча? Я уже понял что ответ 500 грамм будет, но хочу узнать как меняются формулы, а скольжение с мячом равно 0.04м (остальное идентично)

Можно (нужно) из конечной формулы выразить \(m\):\[S = \frac<<\upsilon _0^2>> <<2\mu g<<\left( \right)>^2>>>\]Из этой формулы имеем:\[\upsilon _0^2 = 2\mu gS <\left( \right)^2>\]В правой части раскроем квадрат суммы масс:\[\upsilon _0^2 = 2\mu gS\left( <+ 2mM + > \right)\]Раскроем скобки:\[\upsilon _0^2 = 2\mu gS + 4\mu gSmM + 2\mu gS\]Мы получили квадратное уравнение относительно искомой массы \(m\):\[\left( <2\mu gS – \upsilon _0^2>\right) + 4\mu gSMm + 2\mu gS = 0\]\[D = 16<\mu ^2> – 8\mu gS\left( <2\mu gS – \upsilon _0^2>\right)\]\[D = 8\mu gS\upsilon _0^2\]\[m = \frac<< – 4\mu gSM \pm \sqrt <8\mu gS\upsilon _0^2> >> <<2\left( <2\mu gS – \upsilon _0^2>\right)>>\]Корень со знаком “плюс” – лишний, поскольку масса получается отрицательной (знаменатель отрицательный). Окончательно:\[m = \frac<<4\mu gSM + \sqrt <8\mu gS\upsilon _0^2> >> <<2\left( <\upsilon _0^2 – 2\mu gS>\right)>>\]Численный ответ посчитаете сами
Кстати, если у нас с Вами отличаются пути \(S\), то и масса \(m\) будет разной (не 0,5 кг).

Источник