Удельная теплота конденсации льда

Удельная теплота испарения и конденсации. Физические величины

Содержание:

Для поддержания кипения жидкости её необходимо нагревать – подводить тепловую энергию от огня или нагревательного прибора. Температура вещества и сосуда при этом не повышаются, вместо этого жидкость превращается в пар – переходит в газообразное состояние. (можно ссылку на агрегатные состояния вещества) Удельная теплота испарения – количество передаваемой системе энергии, необходимо для поддержания процесса. Зависит от жидкости, внешних условий, при которых она кипит, в первую очередь, давления.

Удельная теплоемкость парообразования

Величина показывает, сколько тепла необходимо жидкости для её преобразования в газообразное состояние. Измеряется в джоулях на килограмм вещества – Дж/кг.

По закону сохранения энергии, получается, что во время конденсации паров выделяется потраченное на испарение вещества количество энергии. Для подтверждения проводится опыт. В стакан с водой опускается трубка, соединённая со вторым сосудом, где подогревается вода. Пока по трубке в стакан поступает подогретый воздух, показатели термометра практически не изменяются.

Когда вследствие нагрева испаряется вода, пар попадает в трубку, где конденсируется с выделением теплоты, ведь показатели термометра растут. Получается, вода из пара превращается в жидкое состояние с выделением тепловой энергии.

Количество выделяемого тепла равняется внутренней энергии тела: Q = ΔU. Энергия колебания молекул пропорциональна температуре. Величина изменения энергии тела или жидкости равняется сумме изменению теплоты каждой молекулы или атома вещества. Отсюда удельную теплоту парообразования находят по выражению:

Q = ΔU = cmΔT, здесь:

• ΔT – разница температур;
• m – масса вещества;
• c – удельная теплоёмкость вещества.

c = Q / mΔT, измеряется в Дж / кг*К. Показывает, сколько теплоты нужно для нагревания 1 кг вещества на 1 К.

Удельная теплота испарения указывается для жидкости при её постоянном объёме, ведь зависит от условий теплопередачи – работы, сопровождающей процесс испарения. Одинаковая энергия, переданная системе, по-разному изменит его внутреннюю энергию и, соответственно, температуру.

Обозначение удельной теплоты парообразования осуществляется буквой L. По значению величина прямо пропорциональна потраченной на трансформацию – изменение состояния вещества – энергии и обратно пропорциональна его массе:

В физике измеряется в Дж/кг, в химии сводится к количеству вещества – моль/кг.

Для закипающей при температуре 100 °C воды удельная теплота парообразования равняется 2260 Дж/кг.

Задача

1005 Дж тепловой энергии. Какое вещество нагревалось в колбе?

Теплота парообразования вычисляется по формуле: L= Q / m. Подставляем значения в готовую пропорцию и проводим вычисления.

L = 1005 / 1,2 = 837,5 Дж/кг. Воспользуемся таблицей удельной теплоты парообразования.

Вещество	Температура кипения, С 0	Удельная теплота парообразования/конденсации, кДж/кг
Вода	100	2260
Водород	-252,6	448
Азот	-195,8	199
Аммиак	-33,4	1370
Диэтиловый спирт	34,6	380
Этиловый спирт	78,4	837
Ртуть	357	282

В ней полученному значению соответствует этиловый спирт.

Источник

Удельная теплота парообразования и конденсации

Содержание

Твердые кристаллические вещества переходят в жидкое состояние посредством плавления. Чтобы расплавить вещество, необходимо сообщить ему некоторое количество теплоты. И, наоборот, при кристаллизации (переходе жидкости в твердое состояние) энергия выделяется в окружающую среду.

Проведем аналогию с переходом жидкости в пар. Этот переход может быть осуществлен двумя способами: испарением или кипением. Кипение является тем же испарением, но более интенсивным. Очевидно, что для того, чтобы происходил процесс кипения, жидкости необходимо сообщать какое-то количество теплоты. Это количество теплоты будет идти на образование пара.

В данном уроке мы познакомимся с новым определением – удельной теплотой парообразования и конденсации. Вы узнаете формулу для расчета количества теплоты, необходимого для парообразования жидкости и научитесь ею пользоваться.

Удельная теплота парообразования

Вы уже знаете, что кипение происходит при определенной для каждой жидкости температуре. Количество теплоты, которое потребуется сообщить этим жидкостям одинаковой массы для превращения их в пар тоже будет различно.

Опытным путем было выяснено следующее. Если мы возьмем воду массой $1 \space кг$ при температуре $100 \degree C$, то нам потребуется затратить $2.3 \cdot 10^6 \space Дж$ энергии для полного превращения этой воды в пар.

Температура кипения во время всего процесса остается постоянной. Следовательно, нам необходимо подводить к кипящей жидкости определенное количество теплоты. Для воды это энергия в $2.3 \cdot 10^6 \space Дж$.

Удельная теплота парообразования – это физическая величина, показывающая, какое количество теплоты необходимо, чтобы обратить жидкость массой $1 \space кг$ в пар без изменения температуры.

• Обозначается буквой $L$
• Единица измерения удельной теплоты парообразования – $1 \frac<Дж><кг>$
• При температуре кипения внутренняя энергия вещества в парообразном состоянии больше внутренней энергии вещества такой же массы в жидком состоянии

Удельная теплота парообразования некоторых жидкостей

В таблице 1 приведены экспериментально полученные величины удельной теплоты парообразования некоторых жидкостей.

Вещество	$L, \frac<Дж><кг>$
Вода	$2.3 \cdot 10^6$
Аммиак (жидкий)	$1.4 \cdot 10^6$
Спирт	$0.9 \cdot 10^6$
Эфир	$0.4 \cdot 10^6$
Ртуть	$0.3 \cdot 10^6$
Воздух (жидкий)	$0.2 \cdot 10^6$

Таблица 1. Удельная теплота парообразования некоторых веществ (при температуре кипения и нормальном атмосферном давлении)

Удельная теплота парообразования эфира равна $0.4 \cdot 10^6 \frac<Дж><кг>$. Что это означает?

Возьмем $1 \space кг$ эфира при его температуре кипения ($35 \degree C$). Для того, чтобы полностью превратить его в пар, нам потребуется $0.4 \cdot 10^6 \space Дж$.

Обратите внимание, что удельная теплота парообразования показывает количество теплоты, необходимое для превращения жидкости, взятой при ее температуре кипения, в пар.

Удельная теплота конденсации

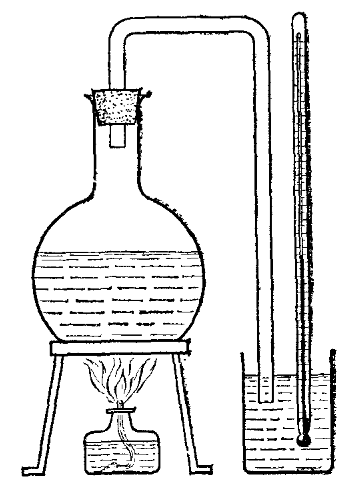
Нужно ли сообщать пару энергию при его конденсации? Давайте рассмотрим простой опыт (рисунок 1).

Нальем в сосуд воду и закроем его пробкой. Через пробку проведем трубку и направим ее на кусочек охлажденного стекла. Доведем воду до кипения с помощью горелки.

Пар, поднимающийся над кипящей водой, будет конденсироваться, соприкасаясь с холодным стеклом. Если мы дотронемся до стекла, то обнаружим, что оно очень сильно нагрелось.

Так энергия пара передается стеклу. В результате этой потери энергии пар конденсируется. Если бы температура стекла была равна температуре пара, то теплопередача бы не происходила, и конденсат не образовывался бы.

Это говорит о том, что при конденсации пар отдает, выделяет энергию.

Более точные опыты также показывают, что

Конденсируясь, пар отдает то количество энергии, которое пошло на его образование.

Значит, при превращении $1 \space кг$ водяного пара в воду при температуре $100 \degree C$ выделяется $2.3 \cdot 10^6 \space Дж$ энергии.

Это довольно большая энергия, поэтому человечество стремится ее использовать. Например, на крупных тепловых электростанциях паром, который уже прошел через турбины, нагревают воду. Ее, в свою очередь, используют для отопления зданий и бытовых нужд.

Расчет количества теплоты, необходимого для парообразования

Чтобы вычислить количество теплоты $Q$, необходимое для превращения в пар жидкости любой массы, взятой при температуре кипения, нужно удельную теплоту парообразования $L$ умножить на массу $m$:
$Q = Lm$.

Из этой формулы при расчетах мы можем выражать массу ($m = \frac$) и удельную теплоту парообразования ($L = \frac$).

Для расчета количества теплоты, которое выделит пар массой $m$ при температуре кипения в ходе конденсации, используется эта же формула.

Примеры задач

1. У вас есть вода массой $2 \space кг$ с температурой $20 \degree C$. Рассчитайте, какое количество энергии потребуется для ее превращения в пар.

Дано:
$m = 2 \space кг$
$t_1 = 20 \degree C$
$t_2 = 100 \degree C$
$c = 4200 \frac<Дж><кг \cdot \degree C>$
$L = 2.3 \cdot 10^6 \frac<Дж><кг>$

$Q – ?$

Показать решение и ответ

Решение:

Сначала нам потребуется нагреть воду до температуры кипения, затратив на это количество энергии $Q_1$:
$Q_1 = cm (t_2 – t_1)$.

$Q_1 = 4200 \frac<Дж> <кг \cdot \degree C>\cdot 2 \space кг \cdot (100 \degree C – 20 \degree C) = 8400 \frac<Дж> <\degree C>\cdot 80 \degree C = 672 \space 000 \space Дж \approx 0.7 \cdot 10^6 \space Дж$.

Теперь рассчитаем количество энергии $Q_2$, затраченное для превращения воды в пар:
$Q_2 = Lm$.

$Q_2 = 2.3 \cdot 10^6 \frac<Дж> <кг>\cdot 2 \space кг = 4.6 \cdot 10^6 \space Дж$.

Рассчитаем общее количество энергии, которое нам потребуется:
$Q = Q_1 + Q_2 = 0.7 \cdot 10^6 \space Дж + 4.6 \cdot 10^6 \space Дж = 5.3 \cdot 10^6 \space Дж$.

Ответ: $Q = 5.3 \cdot 10^6 \space Дж$.

1. Вычислите, какое количество энергии выделится при охлаждении водяного пара массой $2 \space кг$ от $100 \degree C$ до $0 \degree C$.

Дано:
$m = 2 \space кг$
$t_1 = 100 \degree C$
$t_2 = 0 \degree C$
$c = 4200 \frac<Дж><кг \cdot \degree C>$
$L = 2.3 \cdot 10^6 \frac<Дж><кг>$

$Q – ?$

Решение:

Температура $100 \degree C$ – это температура парообразования воды и конденсации водяного пара. При понижении температуры пар сначала сконденсируется в жидкость, а жидкость продолжит охлаждаться.
Количество теплоты, выделенное при этом будет равно:
$Q = Q_1 + Q_2$, где
$Q_1$ – количество выделенной теплоты при конденсации пара,
$Q_2$ – количество теплоты, выделенное при охлаждении жидкости до $0 \degree C$.

$Q_1 = Lm$.
$Q_1 = 2.3 \cdot 10^6 \frac<Дж> <кг>\cdot 2 \space кг = 4.6 \cdot 10^6 \space Дж$.

$Q_2 = cm (t_1 – t_2)$.
$Q_2 = 4200 \frac<Дж> <кг \cdot \degree C>\cdot 2 \space кг \cdot (100 \degree C – 0 \degree C) = 8400 \frac<Дж> <\degree C>\cdot 100 \degree C = 840 \space 000 \space Дж \approx 0.8 \cdot 10^6 \space Дж$.

$Q = 4.6 \cdot 10^6 \space Дж + 0.8 \cdot 10^6 \space Дж= 5.4 \cdot 10^6 \space Дж$.

Ответ: $Q = 5.4 \cdot 10^6 \space Дж$.

1. Из чайника выкипела вода объемом $0.5 \space л$. Начальная температуры этой воды составляла $10 \degree C$. Какое количество энергии оказалось излишне затраченным? Плотность воды – $1000 \frac<кг><м^3>$.

Дано:
$V = 0.5 \space л$
$\rho = 1000 \frac<кг><м^3>$
$L = 2.3 \cdot 10^6 \frac<Дж><кг>$

СИ:
$0.5 \cdot 10^ <-3>\space м^3$

$Q – ?$

Посмотреть решение и ответ

Решение:

После закипания воды в чайнике огонь выключают. Если его не выключить, то процесс кипения продолжится, и вода из чайника будет испаряться. Так как превращение воды в пар не является целью кипячения воды, энергию, которая ушла на парообразование можно считать излишне затраченной. Рассчитаем ее по формуле: $Q = Lm$.

Массу мы можем выразить через плотность и объем:
$m = \rho V$.

Тогда наша формула примет вид:
$Q = L\rho V$.

$Q = 2.3 \cdot 10^6 \frac<Дж> <кг>\cdot 1000\frac<кг> <м^3>\cdot 0.5 \cdot 10^ <-3>\space м^3 = 2.3 \cdot 10^6 \frac<Дж> <кг>\cdot 0.5 \space кг = 1.15 \cdot 10^6 \space Дж$.

Ответ: $Q = 1.15 \cdot 10^6 \space Дж$.

Источник

Удельная теплота конденсации льда

Задача № 1. Какое количество энергии требуется для обращения воды массой 150 г в пар при температуре 100 °С?

Задача № 2. Какое количество энергии требуется для превращения воды массой 2 кг, взятой при температуре 20 °С, в пар?

Задача № 3. Какое количество энергии нужно затратить, чтобы воду массой 5 кг, взятую при температуре 0 °С, довести до кипения и испарить её?

Задача № 4. Какую энергию нужно затратить, чтобы расплавить кусок свинца массой 8 кг, взятый при температуре 27 °С?

Задача № 5. Какое количество энергии требуется для превращения в пар спирта массой 200 г, взятого при температуре 18 °С?

Задача № 6. Какое количество энергии требуется для превращения в пар воды массой 5 кг, взятой при температуре 20 °С?

Задача № 7. Какое количество теплоты необходимо сообщить воде массой 10 г, взятой при температуре 0 °С, для того, чтобы нагреть ее до температуры кипения и испарить?

Задача № 8. Из чайника выкипела вода объемом 0,5 л, начальная температура которой была равна 10 °С. Какое количество теплоты оказалось излишне затраченным?

Задача № 9. Кофейник вместимостью 1,2 л заполнили водой при температуре 15 °С и поставили на плиту. Какое количество теплоты пошло на нагревание и кипение воды, если после снятия с плиты в результате испарения в кофейнике объем воды стал на 50 см 3 меньше? (Изменение плотности воды с изменением температуры не учитывать.)

Задача № 10. Какое количество теплоты выделяется при конденсации водяного пара массой 10 кг при температуре 100 °С и охлаждении образовавшейся воды до 20 °С?

Задача № 11. Какое количество теплоты необходимо, чтобы из льда массой 2 кг, взятого при температуре -10 °С, получить пар при 100 °С?

Задача № 12. Сколько энергии понадобится, чтобы полностью испарить 100 грамм ртути, взятой при температуре 27 °С?

Краткая теория для решения Задачи на парообразование и конденсацию.

Это конспект по теме «Задачи на парообразование и конденсацию». Выберите дальнейшие действия:

Источник