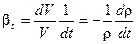Удельная теплота нагревания льда равна

Физико-механические и теплофизические свойства льда и шуги

Плотность льда, образовавшегося при кристаллизации пресной воды при 0°С и нормальном давлении, составляет в среднем 917 кг/м 3 . Следовательно, плотность пресноводного льда меньше плотности воды. Плотность льда зависит от его структуры, температуры и в большей степени от его пористости (во льду рек и водоемов почти всегда наблюдаются пузырьки воздуха).

С понижением температуры плотность льда увеличивается, а объем уменьшается. В зависимости от температуры плотность и удельный объем льда можно рассчитать по формулам Вейнберга:

ρ = 917 (1 — 0,000158t)(1 — n); (2.33)

где п — пористость льда.

Из (2.33) следует, что, зная плотность льда (r_л,n=0.=917кг/м 3 ), можно определить его пористость

Плотность льда, образовавшегося в результате замерзания соленой воды(морской или озерной), зависит не только от его температуры и количества воздушных пузырьков в нем, но еще и от содержания солей в прослойках между кристаллами льда и от количества в этих прослойках рассола. И то и другое зависит от быстроты замерзания и от возраста льда. Старый морской лед имеет иное распределение солености по глубине, чем молодой. В морском льду рассол стекает вниз по неизбежным во льду трещинам, вследствие чего соленость его непрерывно изменяется во времени. Соленость льда всегда меньше солености воды, из которой он образовался.

Плотность морского льда увеличивается по мере увеличения солености воды и уменьшается с увеличением содержания воздушных пузырьков.

Расширение (сжатие) характеризуется коэффициентом объемного расширения, который равен отношению относительного изменения объема вещества V к изменению температуры t и определяется по формуле

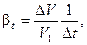
Коэффициент объемного расширения (сжатия) льда β_t можно принять с достаточно высокой точностью постоянным и равным

0,158·10 -3 °С -1 . Коэффициент линейного расширения (сжатия) соответственно равен a_t = β_t/3 = 0,053·10 -3 °С -1 .

Лед течет при напряжениях в ледяном покрове P > 5·10 4 Па. Характеристикой его текучести является коэффициент вязкости μ. Этот коэффициент определяется в зависимости от температуры льда по формулам:

при t ≥ -20°С

μ = (11,6 – 0,978t +0,293t 2 ) 10 11 , (2.35)

при t 11 , (2.36)

где t — средняя температура слоя льда.

ДЛЯ ВОДЫ при t = 0 0 μ = 1,793·10 3 Па·с

Коэффициент μ также сильно зависит от структуры льда, характера нагрузки и продолжительности ее приложения.

Плавление льда при постоянном внешнем давлении протекает при определенной температуре, называемой температурой плавления — t_пл.

Температура плавления льда определяется давлением, при котором он находится; она понижается с повышением давления (рис. 2.2). Зависимость ее от давления описывается уравнением Клапейрона—Клаузиуса, а также может быть представлена следующей формулой:

(2.37)

При давлении до 10 7 Па эту зависимость можно заменить линейной:

Рис. 2.2. Ход температуры во льду во времени при подводе к нему теплоты [8]

1 — 2 — нагревание льда; 2 — 3 — плавление льда: 3 — 4— нагревание воды; t_пл —температура плавления льда.

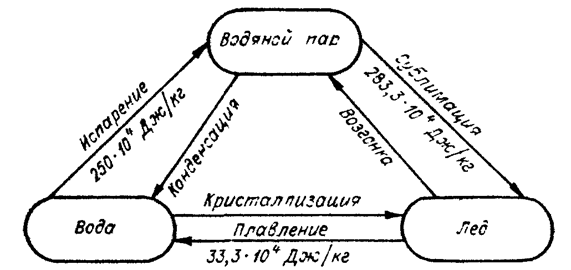
Плавление льда при атмосферном давлении происходит при температуре 0,01°С (в практических расчетах принимают 0°С).Количество теплоты, которое необходимо сообщить 1 кг льда, находящемуся при температуре плавления, для превращения его в воду, называют удельной теплотой плавления L_пл. Удельная теплота плавления пресноводного льда при нормальных условиях равна удельной теплоте кристаллизации воды 33,3·10 4 Дж/кг (п. 2.1).

Удельная теплота сублимации (возгонки) льда (рис. 2.3) равна сумме удельной теплоты плавления льда и удельной теплоты испарения воды; при 0°С она равна

L_воз = 33,3·10 4 + 250·10 4 = 283,3·10 4 Дж/кг.

Коэффициент теплопроводности льда λ принимают в среднем равным 2,24Вт/(м·°С). С повышением температуры λуменьшается незначительно и линейно.

Удельную теплоемкость льда вычисляют по формуле Б. П. Вейнберга:

c = 2,12 (1 + 0,0037t). (2.39)

При t=0°С теплоемкость льда c = 2,12 кДж/(кг·°С).

Рис. 2.3. Схема изменения агрегатного состояния воды [8]

Таблица 2.4

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)

Источник

Удельная теплоемкость вещества

О чем эта статья:

Нагревание и охлаждение

Эти два процесса знакомы каждому. Вот нам захотелось чайку, и мы ставим чайник, чтобы нагреть воду. Или ставим газировку в холодильник, чтобы охладить.

Логично предположить, что нагревание — это увеличение температуры, а охлаждение — ее уменьшение. Все, процесс понятен, едем дальше.

Но не тут-то было: температура меняется не «с потолка». Все завязано на таком понятии, как количество теплоты. При нагревании тело получает количество теплоты, а при нагревании — отдает.

• Количество теплоты — энергия, которую получает или теряет тело при теплопередаче.

В процессах нагревания и охлаждения формулы для количества теплоты выглядят так:

Нагревание

Охлаждение

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

В этих формулах фигурирует и изменение температуры, о котором мы сказали выше, и удельная теплоемкость, речь о которой пойдет дальше.

А вот теперь поговорим о видах теплопередачи.

Виды теплопередачи

• Теплопередача — это физический процесс передачи тепловой энергии от более нагретого тела к менее нагретому.

Здесь все совсем несложно, их всего три: теплопроводность, конвекция и излучение.

Теплопроводность

Тот вид теплопередачи, который можно охарактеризовать, как способность тел проводить энергию от более нагретого тела к менее нагретому.

Речь о том, чтобы передать тепло с помощью соприкосновения. Признавайтесь, грелись же когда-нибудь возле батареи. Если вы сидели к ней вплотную, то согрелись вы благодаря теплопроводности. Обниматься с котиком, у которого горячее пузо, тоже эффективно.

Порой мы немного перебарщиваем с возможностями этого эффекта, когда на пляже ложимся на горячий песок. Эффект есть, только не очень приятный. Ну а ледяная грелка на лбу дает обратный эффект — ваш лоб отдает тепло грелке.

Конвекция

Когда мы говорили о теплопроводности, мы приводили в пример батарею. Теплопроводность — это когда мы получаем тепло, прикоснувшись к батарее. Но все вещи в комнате к батарее не прикасаются, а комната греется. Здесь вступает конвекция.

Дело в том, что холодный воздух тяжелее горячего (холодный просто плотнее). Когда батарея нагревает некий объем воздуха, он тут же поднимается наверх, проходит вдоль потолка, успевает остыть и спуститься обратно вниз — к батарее, где снова нагревается. Таким образом, вся комната равномерно прогревается, потому что все более горячие потоки сменяют все менее холодные.

Излучение

Пляж мы уже упоминали, но речь шла только о горячем песочке. А вот тепло от солнышка — это излучение. В этом случае тепло передается через волны.

Обоими способами. То тепло, которое мы ощущаем непосредственно от камина (когда лицу горячо, если вы расположились слишком близко к камину) — это излучение. А вот прогревание комнаты в целом — это конвекция.

Удельная теплоемкость: понятие и формула для расчета

Формулы количества теплоты для нагревания и охлаждения мы уже разбирали, но давайте еще раз:

Нагревание

Охлаждение

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

В этих формулах фигурирует такая величина, как удельная теплоемкость. По сути своей — это способность материала получать или отдавать тепло.

С точки зрения математики удельная теплоемкость вещества — это количество теплоты, которое надо к нему подвести, чтобы изменить температуру 1 кг вещества на 1 градус Цельсия:

Удельная теплоемкость вещества

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

Также ее можно рассчитать через теплоемкость вещества:

Удельная теплоемкость вещества

c — удельная теплоемкость вещества [Дж/кг*˚C]

C — теплоемкость вещества [Дж/˚C]

Величины теплоемкость и удельная теплоемкость означают практически одно и то же. Отличие в том, что теплоемкость — это способность всего вещества к передаче тепла. То есть формулу количества теплоты для нагревания тела можно записать в таком виде:

Количество теплоты, необходимое для нагревания тела

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

Таблица удельных теплоемкостей

Удельная теплоемкость — табличная величина. Часто ее указывают в условии задачи, но при отсутствии в условии — можно и нужно воспользоваться таблицей. Ниже приведена таблица удельных теплоемкостей для некоторых (многих) веществ.

Источник

Плотность льда и снега, теплопроводность, теплоемкость льда

Плотность, теплопроводность и теплоемкость льда в зависимости от температуры

В таблице приведены значения плотности, теплопроводности, удельной теплоемкости льда в зависимости от температуры в интервале от 0 до -100°С.

По данным таблицы видно, что с понижением температуры удельная теплоемкость льда уменьшается, а теплопроводность и плотность льда, напротив, растут. Например, при температуре 0°С плотность льда имеет значение 916,2 кг/м 3 , а при температуре минус 100°С его плотность становится равной 925,7 кг/м 3 .

Значение удельной теплоемкости льда при 0°С составляет 2050 Дж/(кг·град). При снижении температуры льда с -5 до -100°С его удельная теплоемкость снижается в 1,45 раза. Теплоемкость льда в два раза меньше значения этой величины у воды.

Теплопроводность льда при понижении его температуры с 0 до минус 100°С увеличивается с 2,22 до 3,48 Вт/(м·град). Лед более теплопроводен, чем вода — он может проводить в 4 раза больше тепла при одинаковых граничных условиях.

Следует отметить, что плотность льда меньше плотности воды, однако с понижением температуры плотность льда растет и при приближении к абсолютному нулю температуры плотность льда становится близка к величине плотности воды.

Таблица плотности, теплопроводности и теплоемкости льда

Температура, °С	Плотность, кг/м 3	Теплопроводность, Вт/(м·град)	Теплоемкость, Дж/(кг·град)
0.01 (Вода)	999,8	0,56	4212
0	916,2	2,22	2050
-5	917,5	2,25	2027
-10	918,9	2,30	2000
-15	919,4	2,34	1972
-20	919,4	2,39	1943
-25	919,6	2,45	1913
-30	920,0	2,50	1882
-35	920,4	2,57	1851
-40	920,8	2,63	1818
-50	921,6	2,76	1751
-60	922,4	2,90	1681
-70	923,3	3,05	1609
-80	924,1	3,19	1536
-90	924,9	3,34	1463
-100	925,7	3,48	1389

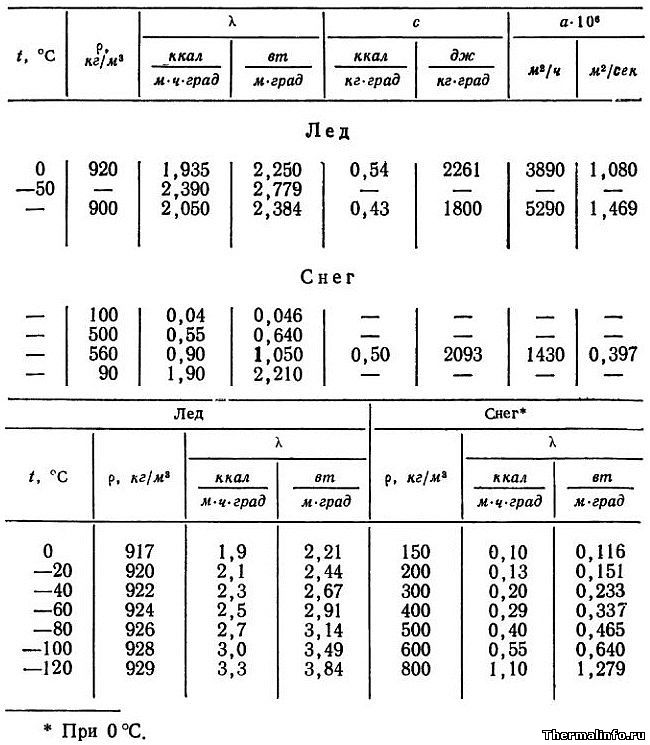
Теплофизические свойства льда и снега

В таблице представлены следующие свойства льда и снега:

• плотность льда, кг/м 3 ;
• теплопроводность льда и снега, ккал/(м·час·град) и Вт/(м·град);
• удельная массовая теплоемкость льда, ккал/(кг·град) и Дж/кг·град);
• коэффициент температуропроводности, м 2 /час и м 2 /сек.

Свойства льда и снега представлены в зависимости от температуры в интервале: для льда от 0 до -120°С; для снега от 0 до -50°С в зависимости от уплотненности (плотности). Температуропроводность льда и снега в таблице приведена с множителем 10 6 . Например, температуропроводность льда при температуре 0°С равна 1,08·10 -6 м 2 /с.

Давление насыщенного пара льда

В таблице приведены значения давления насыщенного пара льда при сублимации (переход льда в пар, миную жидкую фазу) в зависимости от температуры в интервале от 0,01 до -80°С. Из таблицы видно, что с понижением температуры льда давление его насыщенного пара снижается.

Источник